ÁLGEBRA LINEAL

• Las matrices y los determinantes son herramientas del álgebra que facilitan el ordenamiento de datos, así como su manejo.
• Una matriz es una tabla bidimensional de números en cantidades abstractas que pueden sumarse y multiplicarse.
• Una matriz es una tabla cuadrada o rectangular de datos (llamados elementos) ordenados en filas y columnas, donde una fila es cada una de las líneas horizontales de la matriz y una columna es cada una de las líneas verticales.

DEFINICIÓN Una matriz es un arreglo rectangular de números reales, encerrado en grandes paréntesis rectangulares. Las matrices por lo regular se denotan con letras mayúsculas negritas como A, B o C

Multiplicación de una matriz por un escalar La multiplicación de una matriz por un escalar se refiere a la operación de multiplicar la matriz por un número real. Si A [aij] es una matriz m n y c es cualquier número real, el producto cA es una matriz m n obtenida multiplicando cada elemento de A por la constante  

41. (Valoración de inventarios) Un comerciante de televisores a color tiene cinco televisores de 26 pulgadas, ocho de 20, cuatro televisores de 18 pulgadas y diez de 12. Los televisores de 26 pulgadas se venden en $650 cada uno, los de 20 en $550 cada uno, los televisores de 18 pulgadas en $500 cada uno y los de 12 se venden en $300 cada uno. Exprese el precio de venta total de su existencia de televisores como el producto de dos matrices.

BIOGRAFÍA GAUSS -JORDAN 

Nació en Ellwangen / Wuerttemberg, al sur de Alemania en el año 1842.En realidad fue un geodesista

Topógrafo alemán que en una obra suya utilizó por primera vez Estudió en el Instituto Politécnico de Stuttgart y después de acabar sus estudios en la Universidad ingeniería en las etapas preliminares de construcción de ferrocarriles. Desde 1865 hasta 1868 enseñó en el Instituto Politécnico de Stuttgart como asistente en geode En 1868, cuando tenía 26 años de edad, fue nombrado profesor en Karlsruhe. Durante este periodo Alemania. En 1873 fundó la revista alemana

Journal of Geodesy

y ese mismo año publicó la primera enciclopedia el algoritmo, conocido como método de Gauss

Jordán, para resolver un sistema de problemas de mínimos cuadrados. En 1874, tomó parte en la expedición de Friedrich Gerhard Rohlfs a Libia para realizar el primer Desde 1881 hasta su muerte, fue profesor de la geometría de la geodesia y su práctica en la U. Murió en la ciudad de Hannover (Alemania) en el año 1899.

BIBLIOGRAFIA DE JOHANN CARL FRIEDRICH GAUSS

Johann Carl Friedrich Gauss nació en el ducado de Brunswick, Alemania, el 30 de abril de 1777, en una familia humilde. Su abuelo era un humilde jardinero y repartidor. Su padre logró tener un modesto negocio familiar, pero no podía sufragar los estudios de sus hijos. De pequeño Gauss fue respetuoso y obediente, y ya en su edad adulta nunca criticó a su padre, que era muy estricto y rudo con él y tuvo la intención de hacerlo trabajar desde niño. El padre de Gauss falleció poco después de que Gauss cumpliera 30 años.

Desde muy pequeño, Gauss mostró su talento para los números y las lenguas. Aprendió a leer solo y, sin que nadie lo ayudara, aprendió muy rápido la aritmética elemental desde muy pequeño. En 1784, a los siete años de edad, ingresó a una de las escuelas de primeras letras de Brunswick donde daba clases un maestro rural llamado Büttner, quien corrigió rápidamente su lectura, le enseñó gramática y ortografía del alto alemán estándar. (Ya que la lengua nativa de Gauss era el( bajo alemán), así como caligrafía y perfeccionó su talento matemático y lo animó a continuar el bachillerato, como consta en su carta para que lo aceptaran en el Lyceum; pero que usaba unos métodos severos y una estricta disciplina, lo que desagradaba a alguien tan sensible. Se cuenta la anécdota de que, a los dos años de estar en la escuela, durante la clase de aritmética, el maestro propuso el problema de sumar los números del 1 al 100 (una progresión aritmética). Gauss halló la respuesta correcta casi inmediatamente exclamando Ligget se (ya está, en bajo alemán). Al acabar la hora se comprobaron las soluciones y se vio que la solución de Gauss era correcta, mientras que no lo eran muchas de las de sus compañeros.

A los 12 años ya miraba con cierto recelo los fundamentos de la geometría. A los 14 años, fue presentado ante el duque de Brunswick. Este quedó fascinado por lo que había oído del muchacho, y por su modestia y timidez, por lo que decidió hacerse cargo de todos los gastos de Gauss que permitió asegurar que su educación en el bachillerato llegara a buen fin. Allí conoció al matemático Martin Bartels quien fue su profesor y se aceleraron sus progresos en Matemáticas. Ambos estudiaban juntos, se apoyaban y se ayudaban para descifrar y entender los manuales que tenían sobre álgebra y análisis elemental. En estos años se empezaron a gestar algunas de las ideas y formas de ver las matemáticas, que caracterizaron posteriormente a Gauss. Se dio cuenta, por ejemplo, del poco rigor en muchas demostraciones de los grandes matemáticos que le precedieron, como Newton, Euler, LaGrange y otros más.

Al año siguiente de conocer al duque, Gauss ingresó al Collegium Carolinum para continuar sus estudios, y lo que sorprendió a todos fue su facilidad para las lenguas. Aprendió y dominó el griego y el latín en muy poco tiempo. Estuvo tres años en el Collegium y, al salir, no tenía claro si quería dedicarse a las matemáticas o a la filología. En esta época ya había descubierto su ley de los mínimos cuadrados, lo que indica el temprano interés de Gauss por la teoría de errores de observación y su distribución.

A los 17 tuvo sus primeras ideas intuitivas sobre la posibilidad de otro tipo de geometría. A los 18 años, Gauss se dio a la tarea de completar lo que, a su juicio, habían dejado sin concluir sus predecesores en materia de teoría de números. Así descubrió su pasión por la aritmética, área en la que poco después tuvo sus primeros triunfos. Su gusto por la aritmética prevaleció por toda su vida, ya que para él «La matemática es la reina de las ciencias y la aritmética es la reina de las matemáticas».

MADUREZ Y MUERTE DE GAUSS

En 1796 demostró que se puede dibujar un polígono regular de 17 lados con regla y compás.

Fue el primero en probar rigurosamente el teorema fundamental del álgebra (disertación para su tesis doctoral en (1799), aunque una prueba casi completa de dicho teorema fue hecha por Jean Le Rond d'Alembert anteriormente.

En 1801 publicó el libro Disquisitiones arithmeticae, con seis secciones dedicadas a la teoría, dándole a esta rama de las matemáticas una estructura sistematizada. En la última sección del libro expone su tesis doctoral. Ese mismo año predijo la órbita de Ceres aproximando parámetros por mínimos cuadrados.

En 1809 fue nombrado director del Observatorio de Gotinga. En este mismo año publicó Theoria motus corporum coelestium in sectionibus conicis Solem ambientium describiendo cómo calcular la órbita de un planeta y cómo refinarla posteriormente. Profundizó sobre ecuaciones diferenciales y secciones cónicas.

En 1835 Carl Friedrich Gauss formularía la ley de Gauss, o teorema de Gauss. Esta ley sería una de sus contribuciones más importantes en el campo del electromagnetismo, y de ella derivarían dos de las cuatro ecuaciones de Maxwell.

Gauss murió en Gotinga el 23 de febrero de 1855.

REDUCCIÓN MATRICIAL

EJERCICIO 8-2 

EXPRESIÓN DE SISTEMA EN FORMA MATRICIAL 

LEONARD EULER

Matemático suizo

Nació el 15 de abril de 1707 en Basilea, Suiza. Hijo de un clérigo. Cursó estudios en la Universidad de la ciudad con el matemático suizo Johann Bernoulli. Con sólo 17 años de edad, se graduó Doctor.

En el año 1727, invitado por la emperatriz de Rusia Catalina I, fue miembro del profesorado de la Academia de Ciencias de San Petersburgo. Catedrático de Física en 1730 y de Matemáticas en 1733. En 1741 fue profesor de matemáticas en la Academia de Ciencias de Berlín a petición del rey de Prusia, Federico el Grande.

En su Introducción al análisis de los infinitos (1748), realizó el primer tratamiento analítico completo del álgebra, la teoría de ecuaciones, la trigonometría y la geometría analítica. Trató el desarrollo de series de funciones y formuló la regla por la que sólo las series convergentes infinitas pueden ser evaluadas adecuadamente. También abordó las superficies tridimensionales y demostró que las secciones cónicas se representan mediante la ecuación general de segundo grado en dos dimensiones.

Poseedor de una asombrosa facilidad para los números y el raro don de realizar mentalmente cálculos de largo alcance. Se recuerda que en una ocasión, cuando dos de sus discípulos, al realizar la suma de unas series de diecisiete términos, no estaban de acuerdo con los resultados en una unidad de la quincuagésima cifra significativa, se recurrió a Euler. Este repasó el cálculo mentalmente, y su decisión resultó ser correcta.

Realizó también aportaciones a la astronomía, la mecánica, la óptica y la acústica. Entre sus obras más destacadas se encuentran Instituciones del cálculo diferencial (1755), Instituciones del cálculo integral (1768-1770) e Introducción al álgebra (1770).

Perdió parcialmente la visión antes de cumplir 30 años y se quedó casi ciego al final de su vida. Regresó a San Petersburgo en 1766, donde murió el 18 de septiembre de 1783.

OBRAS

Mechanica, sive motus scientia analytica exposita (1736)

Tentamen novae theoriae musicae (1739)

Solutio problematis ad geometriam situs pertinentis (1741)

Methodus inveniendi líneas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici latissimo sensu accepti (1744)

Introductio in Analysis Infinitorum (1748)

Institutiones Calculi Differentialis (1765)

Theoria motus corporum solidorum seu rigidorum (1765)

Institutiones Calculi Integralis (1768-1770)

Vollständige Anleitung zur Algebra42 (1770)

Lettres à une Princesse d'Allemagne (1768–1772)

Web grafía

http://www.buscabiografias.com/biografia/verDetalle/8693/Leonhard%20Euler

https://www.google.com.co/search?q=matemático+leonhard+euler&source

https://www.google.com.co/search?q=inversa+x+determinante&source=lnms&tbm=

https://es.wikipedia.org/wiki/Regla_de_Cramer

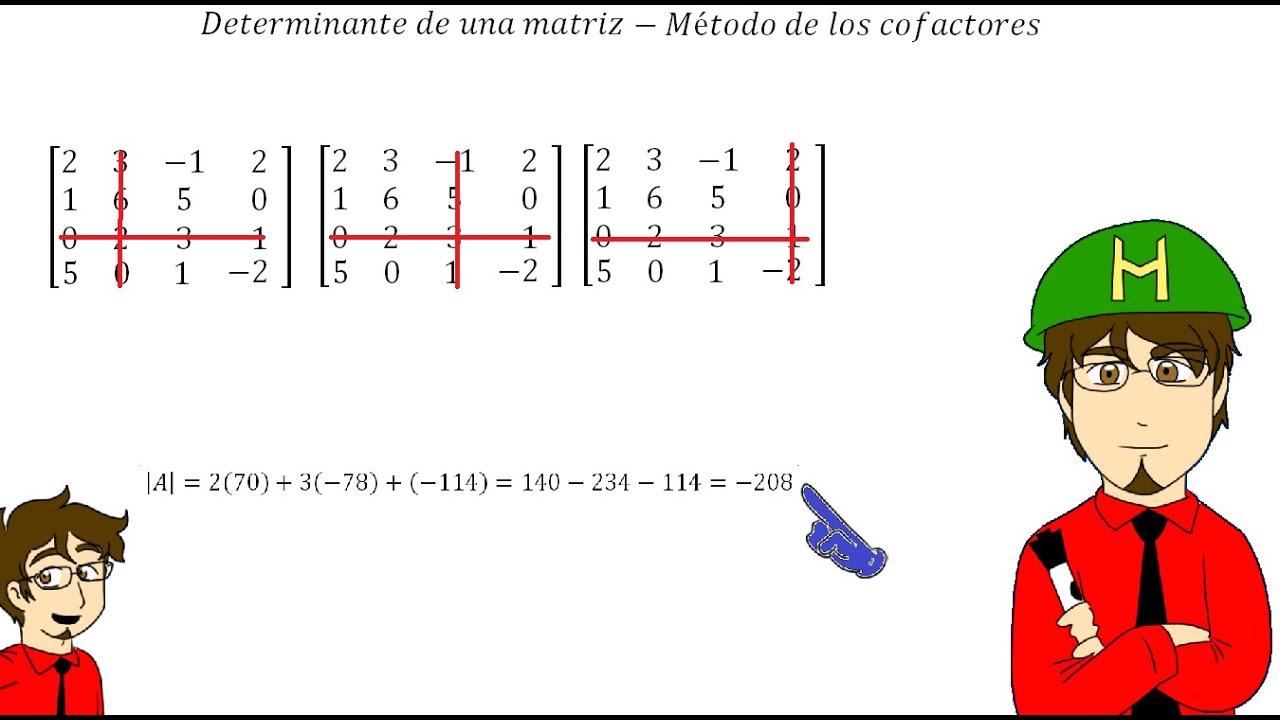
INVERSAS POR DETERMINANTES

 En la sección 9-1 encontramos, mediante operaciones entre renglones la inversa de una matriz no singular. También es posible calcular inversas usando determinantes y, de hecho, en el caso de matrices pequeñas (2 2 o 3 3) este método es más conveniente que la utilización de operaciones entre renglones. DEFINICIÓN Sea A [aij] una matriz de cualquier tamaño. La matriz obtenida intercambiando los renglones y las columnas de A se denomina la transpuesta de A y se denota por AT. El primero, segundo, tercer renglones de A se convierten en la primera, segunda, tercera,..., columnas de AT. E

https://www.youtube.com/watch?v=Ki86UAlP4Dg

MÉTODO INVERSA DETERMINANTE

Regla de Cramer

La regla de Cramer es un teorema del álgebra lineal que da la solución de un sistema lineal de ecuaciones en términos de determinantes. Recibe este nombre en honor a Gabriel Cramer (1704-1752), quien publicó la regla en su Introduction à l'analyse des lignes courbes algébriques de 1750, aunque Colin Maclaurin también publicó el método en su Treatise of Geometry de 1748 (y probablemente sabía del método desde 1729).¹

La regla de Cramer es de importancia teórica porque da una expresión explícita para la solución del sistema. Sin embargo, para sistemas de ecuaciones lineales de más de tres ecuaciones su aplicación para la resolución del mismo resulta excesivamente costosa: computacionalmente, es ineficiente para grandes matrices y por ello no es usado en aplicaciones prácticas que pueden implicar muchas ecuaciones. Sin embargo, como no es necesario pivotar matrices, es más eficiente que la eliminación gaussiana para matrices pequeñas, particularmente cuando son usadas operaciones SIMD.

Si ${\displaystyle \mathbf {Ax} =\mathbf {b} }$ es un sistema de ecuaciones, ${\displaystyle \mathbf {A} }$ es la matriz de coeficientes del sistema, ${\displaystyle \mathbf {x} =(x_{1},\dots ,x_{n})}$ es el vector columna de las incógnitas, y ${\displaystyle \mathbf {b} }$ es el vector columna de los términos independientes, entonces la solución al sistema se presenta así:

${\displaystyle x_{j}={\cfrac {\det(\mathbf {A} _{j})}{\det(\mathbf {A} )}}}$

donde ${\displaystyle \mathbf {A} _{j}}$ es la matriz resultante de reemplazar la j-ésima columna de ${\displaystyle \mathbf {A} }$ por el vector columna ${\displaystyle \mathbf {b} }$. Hágase notar que para que el sistema sea compatible determinado, el determinante de la matriz ${\displaystyle \mathbf {A} }$ ha de ser no nulo.